Ответьте на вопросы теста.

Готовясь к новому учебному году, следует продумать, что в изучаемом предмете было сложным, непонятным, интересным или не очень. Вот этот тест, позволит вам выяснить свое отношение к физике, а значит, новый учебный год будет в этом плане более успешным.

Выпускной 2011

Счастья вам, успехов и достижений, мои дорогие ученики!

Разработки тем курса физики

В этом разделе будут приводиться разработки уроков по разным темам курса школьной физики. Можно готовиться к урокам, повторять материал, учиться решать задачи и все, что нужно на уроках. Работа долгая и кропотливая. Но вместе будем идти к цели. Вопросы по темам можно задавать в комментариях


Кинематика
-первоначальные сведения о движении

Основные понятия кинематики

Движение тела может быть описано полностью, если найден метод определения положения движущегося тела в пространстве в любой момент времени. Выясним, что требуется для полного кинематического описания движения тела.

Прежде всего надо указать тело отсчета, т. е. тело, относительно которого рассматривается изменение положения движущегося тела. Наблюдения показывают (см. § 3), что описание движения (и в частности, ответы на вопросы: движется тело или нет, каковы направление и скорость движения и т. д.) зависит от выбора тела отсчета.

Затем необходимо выбрать способ определения положения движущегося тела относительно тела отчета. При этом, так как тела имеют пространственную протяженность, т. е. определенные размеры, возникает вопрос, когда можно сразу определять положение всего тела, не вдаваясь в то, каким образом движутся его отдельные части?

В случае, когда все точки тела движутся одинаково, для описания движения тела достаточно описать движение какой-либо одной из его точек. Примером такого движения являетсяпоступательное движение. Поступательным называют такое движение, при котором любая прямая, проведенная в теле, перемещается параллельно самой себе.

Нет необходимости описывать движение каждой точки тела и в тех случаях, когда размеры тела можно не учитывать (например, ввиду их малости по сравнению с расстояниями до других тел). Тело, размерами которого в данных условиях можно пренебречь, считая при этом, что вся его масса сосредоточена в одной точке, называют материальной точкой. Очевидно, что при одних условиях данное тело может считаться материальной точкой, а при других - не может.

В дальнейшем при изучении механических движений (если не будет сделано специальных оговорок), говоря о теле, мы всегда будем иметь в виду материальную точку.

Линию, по которой движется материальная точка в пространстве, называют траекторией ее движения. Иными словами, траекторией движения называют совокупность всех последовательных положений, занимаемых материальной точкой при ее движении в пространстве.

Для того чтобы установить положение движущейся материальной точки относительно тела отчета, с ним связывают начало прямоугольной (декартовой) системы координат или точку приложения радиуса-вектора r (рис. 1). Тогда совокупность трех координат х, у, z (или радиус-вектор r) однозначно определяет положение материальной точки в пространстве.

Тело отсчета, связанная с ним координатная система и прибор для измерения времени (часы) образуютсистему отсчета.

Пусть материальная точка движется из начальной точки М1 траектории в конечную точку M₂по дуге М₁М₂ (см. рис. 1). Координаты начальной точки х₁, у₁, z₁. Расстояние, пройденное материальной точкой по ее траектории, т. е. длину дуги |M₁M₂|=Ds; называют длиной пройденного пути.

Проведем из точки M₁ в точку M₂ направленный отрезок Dr. Вектор Dr, соединяющий начальное положение движущейся материальной точки с каким-либо последующим ее положением, называют перемещением материальной точки. Как видно из рис.1, длина пути и перемещение - разные понятия. Длина пути совпадает с перемещением только в том случае, если материальная точка движется по прямой в одну сторону.

Проведя из начала координат в точку М₁ радиус-вектор r₁, а в точку M₂ радиус-вектор r₂, мы увидим, что вектор перемещения Dr равен разности векторов r₂ и r₁, т.е. Dr=r₂-r₁.

Кинематический закон движения

Пусть нам известны система отсчета, начальная точка движения тела и траектория его движения. В этом случае для того, чтобы полностью описать движение тела, необходимо найти способ определения его положения на траектории в любой момент времени, т. е. установить кинематический закон движения тела.

Если положение материальной точки в пространстве задается ее координатами, для описания движения необходимо найти их зависимость от времени, т. е. аналитический вид функции x(t), y(t) и z(t).

Если положение материальной точки задается с помощью радиуса-вектора, для описания ее движения необходимо найти зависимость этого радиуса-вектора от времени, т. е. аналитический вид функции r(t), или же зависимость от времени вектора перемещения этой материальной точки Dr(t).

Кинематический закон движения может быть выражен в трех формах: аналитически (в виде формулы, представляющей собой уравнение данного движения, из которого видно, как изменяются в течение времени координаты тела, его радиус-вектор или же вектор перемещения), таблично (таблицу составляют на основе формулы) и графически.

Таким образом, движение тела (материальной точки) может быть полностью описано кинематически, если известны система отсчета, начальное положение движущегося тела и его перемещение в любой момент времени.

Основные формулы кинематики

Скорость 

Ускорение: 

Нормальное ускорение: 

Касательное ускорение: 

Классический закон сложения скоростей: 

Равномерное прямолинейное движение: 

s = s0 + υt

Равноускоренное прямолинейное движение: 

Свободное падение тел: 

Равномерное движение по окружности: 

T = 2πR/V; ν = 1/T; ω = 2π/T

Движение по окружности: 

a_n – центростремительное ускорение.
- виды механического движения
- методы решения кинематических задач
-вращательное движение
-неравномерное движение
-особенности решения графических задач
-относительность движения
-кинематика свободного падения

Закрепление материала
 - простые задачи
-задачи посложнее
-тест
-проверка знаний 9 класс
- подготовка к ЕГЭ    вариант 1.
вариант 2




и если уж совсем плохо, то можно посмотреть видео с решением задач и ходом рассуждений.

3-D рисунки. Смотрите и удивляйтесь!

 

Эти удивительные рисунки выполнены в специальной технике искажения и наклона, которая позволяет создать иллюзию объёмной картины на плоскости,  если посмотреть на неё с определенного ракурса. Живопись с использованием проекции называется анаморфозом.

 Эту технику использовали средневековые художники (см. например, известную картину Г. Гольбейна Младшего «Послы», 1533 г.).

 Первым  додумался рисовать уникальные объемные картины прямо на городских улицах британский художник Джулиан Бивер


  

Его рисунки можно назвать настоящими произведениями искусства 

Становится модным заказывать объёмные рисунки для рекламы различных продуктов. Стоимость рисунков от 1000 до 20 000 долларов.

У художников нет отбоя  от рекламодателей по всему миру, картинки привлекают огромное число зрителей, а, значит, потенциальных покупателей

Наиболее креативные  люди обзавелись 3D-татуировками на собственном теле

 —  3D-рисунки выглядят объёмными, только если рассматривать их, стоя в определённой позиции. С других позиций фигуры кажутся плоскими,  сильно вытянутыми и непропорциональными – см. ту же картину с противоложной стороны улицы  

Интересные факты

Какой физический эффект был доказан на практике музыкантами, два дня подряд играющими одну ноту?

Австрийский физик Кристиан Допплер в 1842 году теоретически обосновал, что частота колебаний, которую воспринимает наблюдатель, зависит от скорости и направления движения источника волн и наблюдателя относительно друг друга. Через три года голландский метеоролог Христофор Бейс-Баллот взялся доказать это утверждение на практике, для чего нанял паровоз с платформой, посадив на неё двух трубачей, а на перроне разместил нескольких музыкантов с абсолютным слухом. Платформа с трубачами, которые, сменяя друг друга, постоянно держали ноту соль, ездила мимо перрона в течение двух дней. Всё это время наблюдатели отмечали, что слышат разные ноты, в результате чего истинность эффекта Допплера была подтверждена.
Ссылка


ГЛАЗА ДАЛЬТОНА

Речь пойдёт об эксперименте, проведённом по просьбе экспериментатора после его смерти.
Английский учёный Джон Дальтон (1766—1844) памятен нам в основном своими открытиями в области физики и химии, а также первым описанием врождённого недостатка зрения — дальтонизма, при котором нарушено распознавание цветов. 
Сам Дальтон заметил, что страдает этим недостатком, только после того, как в 1790 году увлёкся ботаникой и оказалось, что ему трудно разобраться в ботанических монографиях и определителях. Когда в тексте шла речь о белых или жёлтых цветках, он не испытывал затруднений, но если цветки описывались как пурпурные, розовые или тёмно-красные, все они казались Дальтону неотличимыми от синих. Нередко, определяя растение по описанию в книге, учёному приходилось спрашивать у кого-нибудь: это голубой или розовый цветок? Окружающие думали, что он шутит. Дальтона понимал только его брат, обладавший тем же наследственным дефектом. Сам Дальтон, сравнивая своё цветовосприятие с видением цветов друзьями и знакомыми, решил, что в его глазах имеется какой-то синий светофильтр. И завещал своему лаборанту после смерти извлечь его глаза и проверить, не окрашено ли в голубоватый цвет так называемое стекловидное тело — студенистая масса, заполняющая глазное яблоко?
Лаборант выполнил завещание учёного и не нашёл в его глазах ничего особенного. Он предположил, что у Дальтона, возможно, было что-то не в порядке со зрительными нервами. 
Глаза Дальтона сохранились в банке со спиртом в Манчестерском литературно-философском обществе, и уже в наше время, в 1995 году, генетики выделили и исследовали ДНК из сетчатки. Как и следовало ожидать, в ней обнаружились гены дальтонизма.
Нельзя не упомянуть ещё о двух крайне странных опытах с органами зрения человека. Исаак Ньютон, вырезав из слоновой кости тонкий изогнутый зонд, запускал его себе в глаз и давил им на заднюю сторону глазного яблока. При этом в глазу возникали цветные вспышки и круги, из чего великий физик сделал вывод, что мы видим окружающий мир потому, что свет оказывает давление на сетчатку. В 1928 году один из пионеров телевидения, английский изобретатель Джон Бэйрд, пытался использовать человеческий глаз в качестве передающей камеры, но, естественно, потерпел неудачу. 
ПРЫЖКИ НЬЮТОНА

В детстве Исаак Ньютон (1643—1727) рос довольно хилым и болезненным мальчиком. В играх на свежем воздухе он обычно отставал от сверстников. 

Третьего сентября 1658 года умер Оливер Кромвель, английский революционер, ненадолго ставший полновластным правителем страны. В этот день над Англией пронёсся необычайно сильный ветер. Народ говорил: это сам дьявол прилетал за душой узурпатора! Но в местечке Грэнтем, где в то время жил Ньютон, дети затеяли состязание по прыжкам в длину. Заметив, что прыгать лучше по ветру, чем против него, Исаак обскакал всех соперников.

Позже он занялся опытами: записал, на сколько футов удаётся прыгнуть по ветру, на сколько — против ветра и на какую дальность он может прыгнуть в безветренный день. Так он получил представление о силе ветра, выраженной в футах. Уже став знаменитым учёным, он говорил, что считает эти прыжки своими первыми экспериментами.

Ньютон известен как великий физик, но его первый эксперимент можно отнести скорее к метеорологии.

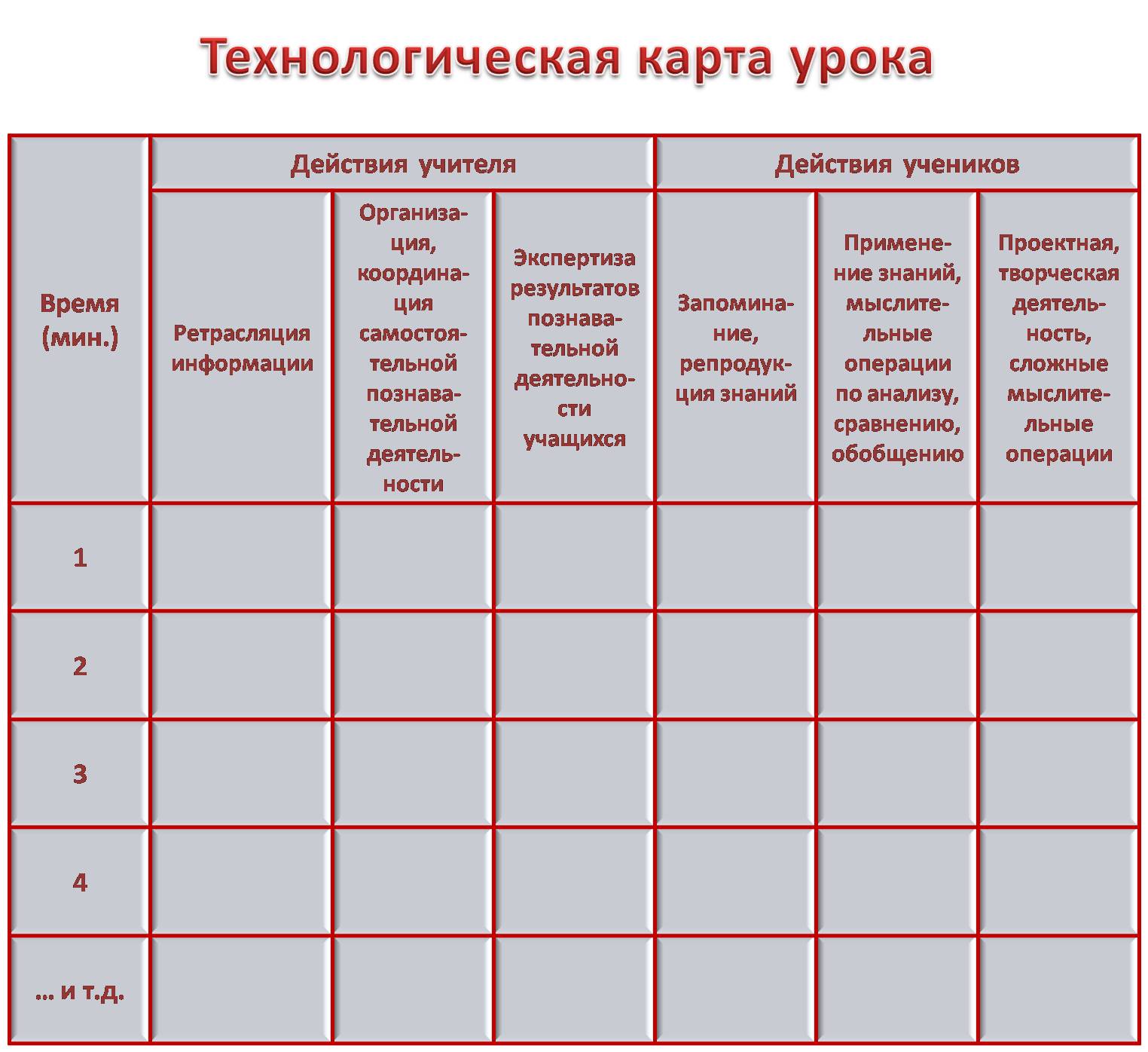
Самоанализ урока

Летнее время – прекрасная пора для “самокопания”, анализа своей профессиональной деятельности, поиска новых возможностей. Иногда это сложно. На первый взгляд учителю кажется, что он всё делает “правильно”. Легче найти оправдание в учениках-”бездарях”, изъянах учебных программ и учебниках, засилии школьной бюрократии и в других объективных причинах профессиональных неудач.
Методические пособия пестрят всякого рода диагностическими материалами для анализа и самоанализа урока. Иногда эти технологические карты и диагностические таблицы занимают не одну страницу. Порой эти разработки сложны для понимания. Да и непрерывная ситуация дефицита времени требует более сжатого и оперативного анализа.

	Самоанализ урока Характеризовать урок нужно обязательно. Особенно, если тема преподносится вами впервые. Научиться ставить «плюсы» и «минусы» урока или проверять, так ли вы проводите анализ урока, можно ... Читать далее

Предлагаю вашему вниманию краткую технологическую карту анализа учебной деятельности на уроке. Она может пригодиться как учителю для самоанализа урока, так и завучу, который оперативно может определить дидактическую направленность урока. 

Если говорить о так называемом “деятельностном подходе” в обучении, то это предполагает необходимость увидеть и описать максимально прозрачно две составляющих: деятельность учителя на уроке и деятельность учащихся.

Данная технологическая карта поможет дать ответ на главный вопрос: насколько данный урок направлен на развитие самостоятельной познавательной активности учащихся. В конечном  счете, быстрый подсчет времени может дать нам ответ на главный вопрос: насколько урок отвечает духу времени.

Сторонники развивающего обучения считают, что

если на уроке монолог учителя, ретрансляция  информации, знаний превышает 8-10 минут, то урок малопродуктивен.

Встречаются и другие уроки. Ученики работают. Работают много. Учителя хвалят своего коллегу за плотность урока, за разнообразие видов ученической деятельности. Однако на деле обращаешь внимание, что проводимые учителем дидактические игры,  викторины, задаваемые им вопросы страдают однобокостью, т.к. направлены лишь на репродукцию знаний, наприпоминание.

Каникулярное время даёт нам прекрасную возможность задуматься над пополнением копилки проблемных ситуаций, формулированием лаконичных учебных заданий на уроке, ориентирующих учеников на сложные мыслительные операции, на проявление ими своих творческих способностей.

Надеюсь, данная технологическая карта будет полезной учителю.

Материал с блога