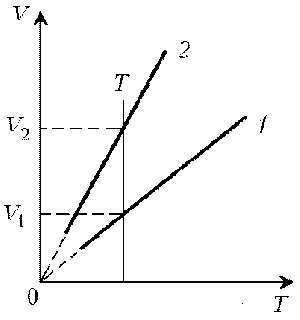вторник, 10 января 2012 г.
понедельник, 9 января 2012 г.
Физические величины в кинематике
С давних пор люди сталкивались с необходимостью определять расстояния, длины предметов, время, площади, объемы, массы и многое другое. Значение измерений возрастало по мере развития общества и развития науки. А чтобы измерять, необходимо было придумать единицы различных физических величин.
Так, например, моряки измеряли путь трубками, т.е. расстоянием, которое проходит судно за время, пока моряк выкурит трубку. В Испании единицей была сигара, в Японии -лошадиный башмак, т.е. путь, который проходила лошадь, пока не износится привязанная к ее копытам соломенная подошва, заменявшая подкову. В Египте распространенной единицей длины был стадий – путь, проходимый мужчиной за время между первым лучом Солнца и появлением на небе всего солнечного диска, примерно за две минуты. У многих народов для определения расстояния использовалась единица длины стрела – дальность полета стрелы. Выражения: “не допускать на ружейный выстрел”, “на пушечный выстрел” - напоминают о подобных единицах длины.
Знаете ли вы, какие существовали и существуют сейчас единицы длины, каково их происхождение?
Локоть – расстояние от конца пальцев до локтевого сустава. Этой единицей пользовались разные народы для измерения длины веревки или ткани .
 На Руси долгое время в качестве единицы длины использовали аршин. Эта мера возникла при торговле с восточными странами. 1 аршин примерно равен 71 см. Многочисленные выражения: “Словно аршин проглотил”, “Мерить на свой аршин” и другие – свидетельствуют о ее широком происхождении.
На Руси долгое время в качестве единицы длины использовали аршин. Эта мера возникла при торговле с восточными странами. 1 аршин примерно равен 71 см. Многочисленные выражения: “Словно аршин проглотил”, “Мерить на свой аршин” и другие – свидетельствуют о ее широком происхождении.
Для измерения маленьких величин длин применяли пядь. Это расстояние между концами расставленных большого и указательного пальцев. Пядь еще называли четвертью. Она равна 18 см и составляла 1/4 аршина, а 1/16 доли аршина равнялся вершок. Вершок равен 4,4 см .

 Так же распространенной единицей длины была сажень. Сажень равнялась 3 аршинам или 2,13 м и она получила название царской. Маховая сажень – размах рук – равна примерно 2,5 аршинам
Так же распространенной единицей длины была сажень. Сажень равнялась 3 аршинам или 2,13 м и она получила название царской. Маховая сажень – размах рук – равна примерно 2,5 аршинам  В странах Западной Европы применяли в качестве единиц длины дюйм и фунт. Дюйм - это длина сустава большого пальца или 2,54 см. Фунт – это средняя длина ступни человека или 30 см
В странах Западной Европы применяли в качестве единиц длины дюйм и фунт. Дюйм - это длина сустава большого пальца или 2,54 см. Фунт – это средняя длина ступни человека или 30 см
Локоть, вершок, пядь, сажень, дюйм, фунт все это единицы длины, соответствующие частям человеческого тела и все они обладают большими недостатками. У различных людей пальцы, ступни и другие части тела имеют разную длину. Чтобы избавиться от произвола, в XIV в. Субъективные единицы заменяют набором объективных единиц. Так, на пример, в 1324 г. в Англии был установлен законный дюйм, равный длине трех приставленных друг к другу ячменных зерен, вытянутых из средней части колоса.
Измеряют все: медики определяют температуру тела, объем легких, рост, пульс пациентов; продавцы взвешивают продукты, отмеряют метры тканей; портные снимают мерку с модниц; музыканты строго выдерживают ритм и темп, считая такты; фармацевты взвешивают порошки и отмеряют в склянки необходимое количество микстуры; учителя физкультуры не расстаются с рулеткой и секундомером, определяя выдающиеся спортивные достижения школьников... Все жители планеты измеряют, прикидывают, оценивают, сверяют, отсчитывают, различают, отмеряют, измеряют и считают, считают, считают...
Каждый из нас, без сомнения, знает, что, прежде чем измерять, нужно установить «единицу, с которой вы будете сравнивать измеряемый отрезок пути или промежуток времени, или массу».
Ясно и другое: о единицах нужно договариваться всем миром, иначе возникнет невообразимая путаница. В играх и то возможны недоразумения: у одного шаг намного короче, у другого – длиннее (Пример: «Будем бить пенальти с семи шагов»). Ученые всего мира предпочитают работать с согласованной и логически последовательной системой единиц измерения. На Генеральной конференции мер и весов в 1960 г. было достигнуто соглашение о международной системе единиц –.Systems International d'Unite's (сокращенно – «единицы измерения СИ»). Эта система включает семь основных единиц измерения, а все остальные единицы измерения производные выводятся из основных умножением или делением одной единицы на другую без числовых пересчётов : длина, время, масса, количество вещества, термодинамическая температура, сила электрического тока, сила света.Международная система единиц является метрической. Это значит, что кратные и дольные единицы образуются из основных всегда одним и тем же способом: умножением или делением на 10. Это удобно, в особенности при записи очень больших и очень малых чисел.
В кинематике основными понятиями являются путь, перемещение, скорость и другие величины. В данной таблице указаны основные кинематические величины, их обозначения и единицы, в которых они выражаются.
Ярлыки:
повторение материала
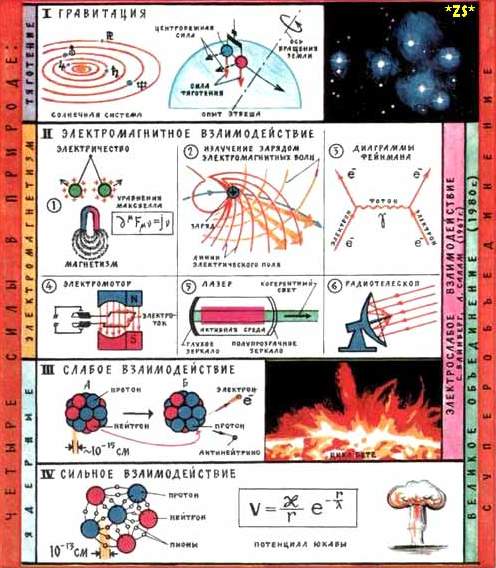
Повторение темы "Силы в природе"
Таблица для повторения темы "Силы в природе"
Воспользуйтесь опорными конспектами от Шороховой О.Г.
1.Силы в природе
2.Сила тяжести
3.Сила упругости
4.Сила трения
5.Вес тела
Ярлыки:
повторение материала
среда, 4 января 2012 г.
Графические задачи на газовые законы
Можно выделить несколько типов графических задач. В задачах первого типа графически задается какой-то изопроцессов в явной или неявной форме. Для решения таких задач можно предложить следующий «план действий»:
1. Установить характер изображенного процесса (если он очевиден).
2. Выбрать (на свое усмотрение) какой-либо из изопроцессов и изобразить его графически (провести изобару, изохору или изотерму).
3. Провести эту линию графика до пересечения с линией (или с линиями) представленного процесса (или процессов).
4. Спроецировать точку (или точки) пересечений этих линий на одну из координатных осей (выбор оси произволен).
5. Рассмотреть состояния данной массы газа, которым соответствуют эти проекции, и, используя известные газовые законы, ответить на поставленный в задаче вопрос.
Пример 1. Какая из двух линий графика соответствует большему давлению данной массы идеального газа?
Решение. Прежде всего установим, что это за линии. Эти линии выражают прямо пропорциональную зависимость между объемом газа и его температурой, а это возможно для идеального газа только при изобарическом процессе, следовательно, изображенные линии графика – изобары.
Проведем изотерму до пересечения с обеими изобарами, а точки их пересечения спроецируем на ось ординат (объемов). Из построения видно, что V2 > V1. Поскольку при изотермическом процессе газ подчиняется закону Бойля–Мариотта: р1V1 = р2V2, то р1 > р2.
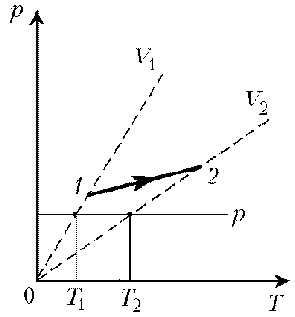 Пример 2. При нагревании идеального газа постоянной массы получена зависимость р(T) при переходе из состояния 1 в состояние 2. Как при этом переходе менялась плотность газа?
Пример 2. При нагревании идеального газа постоянной массы получена зависимость р(T) при переходе из состояния 1 в состояние 2. Как при этом переходе менялась плотность газа?
Решение. Линия графика не описывается ни одним из изопроцессов («неявная форма»). Проведем через начальную и конечную точки линии графика две изохоры.
Проведя еще изобару (или, как вариант, изотерму) и, спроецировав точки ее пересечения с изохорами на ось Т, убедимся, что Т2 > Т1. При изобарическом процессе, по закону Гей-Люссака, V ~ T, следовательно, V2 > V1. А т.к. плотность и объем связаны обратной зависимостью (при данной массе), то r1 > r2, откуда следует, что газ расширялся, а значит, его плотность уменьшилась.
В задачах второго типа в условии задан некий цикл, совокупность процессов, в результате которых данная масса газа возвращается в исходное состояние. Этот цикл может быть задан на разнообразных диаграммах: p, V; p, T; V, T и др. Как правило, в таких задачах требуется представить заданный цикл на других диаграммах. Эти задачи важны при рассмотрении первого закона термодинамики, когда совершается макроскопическая работа и происходит процесс теплообмена. Важно понимать, что цикл – это замкнутый процесс, и он должен быть замкнутым на любой диаграмме.
При решении предлагается следовать следующему алгоритму:
1. Установить характер процесса на данном этапе.
2. Указать закон, по которому протекает процесс.
3. Отметить суть этого закона (как связаны между собой величины).
4. По графику выяснить, как меняется каждая величина.
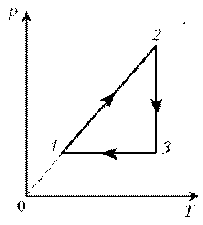
Пример 3. На диаграмме р, T изображен цикл идеального газа постоянной массы. Изобразите его на диаграмме р, V.
Решение. Проведем поэтапный анализ представленного цикла:
1–2: изохорический процесс; закон Шарля; р ~ T; р-возрастает, T-увелич.
2–3: изотермический процесс; закон Бойля–Мариотта; р ~ 1/V; р-уменьшается; V-увеличивается
3–1: изобарический процесс; закон Гей-Люссака; V ~ T; T-уменьшается; V-уменьшается.
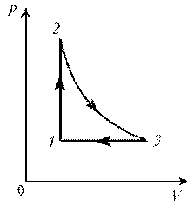 Теперь результаты поэтапного анализа перенесем на диаграмму р, V.
Теперь результаты поэтапного анализа перенесем на диаграмму р, V.
Приведено несколько примеров, но с их помощью можно понять алгоритм решения такого рода задач.
1. Установить характер изображенного процесса (если он очевиден).
2. Выбрать (на свое усмотрение) какой-либо из изопроцессов и изобразить его графически (провести изобару, изохору или изотерму).
3. Провести эту линию графика до пересечения с линией (или с линиями) представленного процесса (или процессов).
4. Спроецировать точку (или точки) пересечений этих линий на одну из координатных осей (выбор оси произволен).
5. Рассмотреть состояния данной массы газа, которым соответствуют эти проекции, и, используя известные газовые законы, ответить на поставленный в задаче вопрос.
Примеры решения задач.
Пример 1. Какая из двух линий графика соответствует большему давлению данной массы идеального газа?
Решение. Прежде всего установим, что это за линии. Эти линии выражают прямо пропорциональную зависимость между объемом газа и его температурой, а это возможно для идеального газа только при изобарическом процессе, следовательно, изображенные линии графика – изобары.
Проведем изотерму до пересечения с обеими изобарами, а точки их пересечения спроецируем на ось ординат (объемов). Из построения видно, что V2 > V1. Поскольку при изотермическом процессе газ подчиняется закону Бойля–Мариотта: р1V1 = р2V2, то р1 > р2.
 Пример 2. При нагревании идеального газа постоянной массы получена зависимость р(T) при переходе из состояния 1 в состояние 2. Как при этом переходе менялась плотность газа?
Пример 2. При нагревании идеального газа постоянной массы получена зависимость р(T) при переходе из состояния 1 в состояние 2. Как при этом переходе менялась плотность газа?Решение. Линия графика не описывается ни одним из изопроцессов («неявная форма»). Проведем через начальную и конечную точки линии графика две изохоры.
Проведя еще изобару (или, как вариант, изотерму) и, спроецировав точки ее пересечения с изохорами на ось Т, убедимся, что Т2 > Т1. При изобарическом процессе, по закону Гей-Люссака, V ~ T, следовательно, V2 > V1. А т.к. плотность и объем связаны обратной зависимостью (при данной массе), то r1 > r2, откуда следует, что газ расширялся, а значит, его плотность уменьшилась.
В задачах второго типа в условии задан некий цикл, совокупность процессов, в результате которых данная масса газа возвращается в исходное состояние. Этот цикл может быть задан на разнообразных диаграммах: p, V; p, T; V, T и др. Как правило, в таких задачах требуется представить заданный цикл на других диаграммах. Эти задачи важны при рассмотрении первого закона термодинамики, когда совершается макроскопическая работа и происходит процесс теплообмена. Важно понимать, что цикл – это замкнутый процесс, и он должен быть замкнутым на любой диаграмме.
При решении предлагается следовать следующему алгоритму:
1. Установить характер процесса на данном этапе.
2. Указать закон, по которому протекает процесс.
3. Отметить суть этого закона (как связаны между собой величины).
4. По графику выяснить, как меняется каждая величина.
Пример 3. На диаграмме р, T изображен цикл идеального газа постоянной массы. Изобразите его на диаграмме р, V.
Решение. Проведем поэтапный анализ представленного цикла:
1–2: изохорический процесс; закон Шарля; р ~ T; р-возрастает, T-увелич.
2–3: изотермический процесс; закон Бойля–Мариотта; р ~ 1/V; р-уменьшается; V-увеличивается
3–1: изобарический процесс; закон Гей-Люссака; V ~ T; T-уменьшается; V-уменьшается.
 Теперь результаты поэтапного анализа перенесем на диаграмму р, V.
Теперь результаты поэтапного анализа перенесем на диаграмму р, V.Приведено несколько примеров, но с их помощью можно понять алгоритм решения такого рода задач.
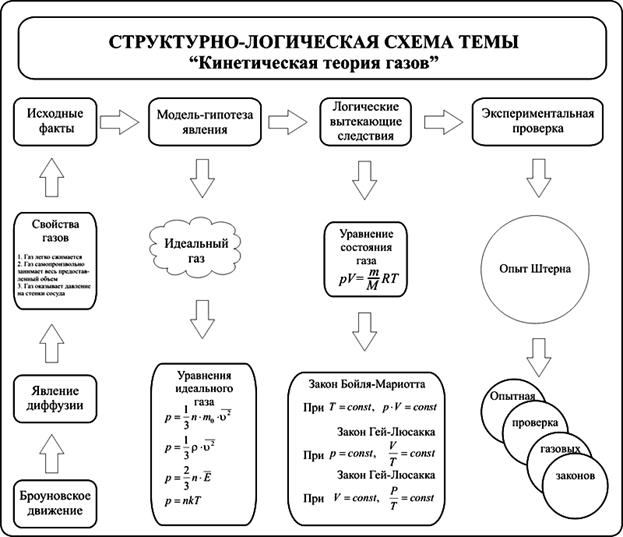
Материал к уроку "Газовые законы"
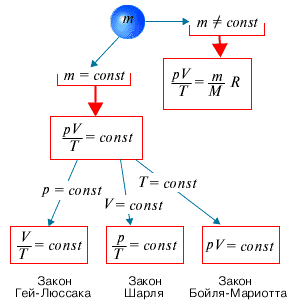
С помощью уравнения состояния идеального газа можно исследовать процессы, в которых масса газа и один из параметров - давление, объем или температура - остается постоянным, а изменяются только остальные два и получить теоретически газовые законы для этих условий изменения состояния газа.
Такие процессы называют изопроцессами. Законы, описывающие изопроцессы, были открыты задолго до теоретического вывода уравнения состояния идеального газа.
Изотермический процесс - процесс изменения состояния системы при постоянной температуре.
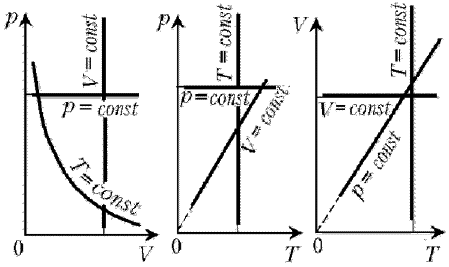
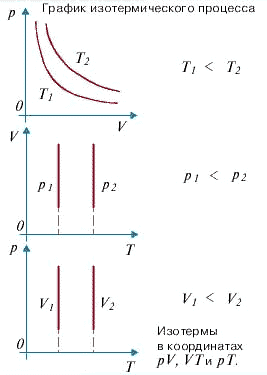
Для данной массы газа произведение давления газа на его объем постоянно, если температура газа не меняется. Это закон Бойля - Мариотта. Для того, чтобы температура газа оставалась в процессе неизменной, необходимо, чтобы газ мог обмениваться теплотой с внешней большой системой - термостатом. Роль термостата может играть внешняя среда (воздух атмосферы). Согласно закону Бойля-Мариотта, давление газа обратно пропорционально его объему: P1V1=P2V2=const. Графическая зависимость давления газа от объема изображается в виде кривой (гиперболы), которая носит название изотермы. Разным температурам соответствуют разные изотермы.
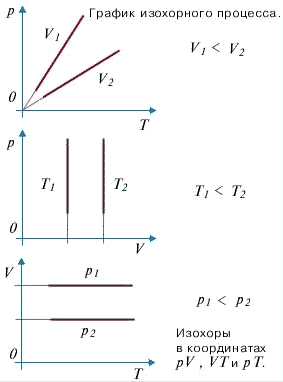 Изохорный процесс - процесс изменения состояния системы при постоянном объеме. Для данной массы газа отношение давления газа к его температуре остается постоянным, если объем газа не меняется. Этот газовый закон Шарля.
Согласно закону Шарля, давление газа прямо пропорционально его температуре: P/T=const.
Изохорный процесс - процесс изменения состояния системы при постоянном объеме. Для данной массы газа отношение давления газа к его температуре остается постоянным, если объем газа не меняется. Этот газовый закон Шарля.
Согласно закону Шарля, давление газа прямо пропорционально его температуре: P/T=const.
Графически эта зависимость в координатах P-Т изображается в виде прямой, выходящей из точки Т=0. Эту прямую называют изохорой. Разным объемам соответствуют разные изохоры. Закон Шарля не соблюдается в области низких температур, близких и температуре сжижения (конденсации) газов.
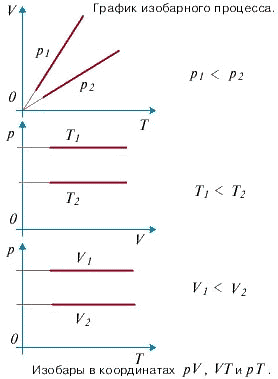 Изобарный процесс - процесс изменения состояния системы при постоянном давлении. Для газа данной массы отношение объема газа к его температуре остается постоянным, если давление газа не меняется. Это закон Гей-Люссака.
Согласно закону Гей-Люссака, объем газа прямо пропорционален его температуре: V/T=const.
Изобарный процесс - процесс изменения состояния системы при постоянном давлении. Для газа данной массы отношение объема газа к его температуре остается постоянным, если давление газа не меняется. Это закон Гей-Люссака.
Согласно закону Гей-Люссака, объем газа прямо пропорционален его температуре: V/T=const.
Графически эта зависимость в координатах V-T изображается в виде прямой, выходящей из точки Т=0. Эту прямую называют изобарой. Разным давлениям соответствуют разные изобары. Закон Гей-Люссака, как и закон Шарля, не соблюдается в области низких температур, близких к температуре сжижения (конденсации) газов. Законы Бойля - Мариотта, Гей-Люссака и Шарля называют частными газовыми законами. Они являются частными случаями объединенного газового закона: Отношение произведения давления газа и объема к температуре для данной массы газа - величина постоянная: PV/T=const.
Отличное пособие размещено здесь
Варианты самостоятельных работ
Приемы решения задач в одной таблице от Рожковой Г.И.
Такие процессы называют изопроцессами. Законы, описывающие изопроцессы, были открыты задолго до теоретического вывода уравнения состояния идеального газа.
Изотермический процесс - процесс изменения состояния системы при постоянной температуре.
Для данной массы газа произведение давления газа на его объем постоянно, если температура газа не меняется. Это закон Бойля - Мариотта. Для того, чтобы температура газа оставалась в процессе неизменной, необходимо, чтобы газ мог обмениваться теплотой с внешней большой системой - термостатом. Роль термостата может играть внешняя среда (воздух атмосферы). Согласно закону Бойля-Мариотта, давление газа обратно пропорционально его объему: P1V1=P2V2=const. Графическая зависимость давления газа от объема изображается в виде кривой (гиперболы), которая носит название изотермы. Разным температурам соответствуют разные изотермы.
 Изохорный процесс - процесс изменения состояния системы при постоянном объеме. Для данной массы газа отношение давления газа к его температуре остается постоянным, если объем газа не меняется. Этот газовый закон Шарля.
Согласно закону Шарля, давление газа прямо пропорционально его температуре: P/T=const.
Изохорный процесс - процесс изменения состояния системы при постоянном объеме. Для данной массы газа отношение давления газа к его температуре остается постоянным, если объем газа не меняется. Этот газовый закон Шарля.
Согласно закону Шарля, давление газа прямо пропорционально его температуре: P/T=const. Графически эта зависимость в координатах P-Т изображается в виде прямой, выходящей из точки Т=0. Эту прямую называют изохорой. Разным объемам соответствуют разные изохоры. Закон Шарля не соблюдается в области низких температур, близких и температуре сжижения (конденсации) газов.
 Изобарный процесс - процесс изменения состояния системы при постоянном давлении. Для газа данной массы отношение объема газа к его температуре остается постоянным, если давление газа не меняется. Это закон Гей-Люссака.
Согласно закону Гей-Люссака, объем газа прямо пропорционален его температуре: V/T=const.
Изобарный процесс - процесс изменения состояния системы при постоянном давлении. Для газа данной массы отношение объема газа к его температуре остается постоянным, если давление газа не меняется. Это закон Гей-Люссака.
Согласно закону Гей-Люссака, объем газа прямо пропорционален его температуре: V/T=const.
Графически эта зависимость в координатах V-T изображается в виде прямой, выходящей из точки Т=0. Эту прямую называют изобарой. Разным давлениям соответствуют разные изобары. Закон Гей-Люссака, как и закон Шарля, не соблюдается в области низких температур, близких к температуре сжижения (конденсации) газов. Законы Бойля - Мариотта, Гей-Люссака и Шарля называют частными газовыми законами. Они являются частными случаями объединенного газового закона: Отношение произведения давления газа и объема к температуре для данной массы газа - величина постоянная: PV/T=const.
Отличное пособие размещено здесь
Варианты самостоятельных работ
Подписаться на:
Комментарии (Atom)