При неравномерном движении скорость тела с течением времени изменяется. Рассмотрим самый простой случай неравномерного движения.
Движение, при котором скорость тела за любые равные промежутки времени изменяется на одно и то же значение, называют равноускоренным.
Например, если за каждые 2 с скорость тела изменялась на 4 м/с, то движение тела является равноускоренным. Модуль скорости при таком движении может как увеличиваться, так и уменьшаться.
2. Пусть в начальный момент времени t0 = 0 скорость тела равна v0. В некоторый момент времени tона стала равной v. Тогда изменение скорости за промежуток времени t – t0 = t равно v– v0, а за единицу времени — . Это отношение называется ускорением. Ускорение характеризует быстроту изменения скорости .
Ускорением тела при равноускоренном движении называют векторную физическую величину, равную отношению изменения скорости тела к промежутку времени, за который это изменение произошло.
Единица ускорения в СИ — метр на секунду в квадратеЗа единицу ускорения принимают ускорение такого равноускоренного движения, при котором скорость тела за 1 с изменяется на 1 м/с.
3. Поскольку ускорение — величина векторная, необходимо выяснить, как оно направлено.
 Пусть автомобиль движется прямолинейно, имея начальную скорость v0 (скорость в момент времени t = 0) и скорость v в некоторый момент времени t. Модуль скорости автомобиля возрастает. На рисунке изображены вектор скорости автомобиля. Из определения ускорения, следует, что вектор ускорения направлен в ту же сторону, что и разность векторов v – v0. Следовательно в данном случае направление вектора ускорения совпадает с направлением движения тела (с направлением вектора скорости).
Пусть автомобиль движется прямолинейно, имея начальную скорость v0 (скорость в момент времени t = 0) и скорость v в некоторый момент времени t. Модуль скорости автомобиля возрастает. На рисунке изображены вектор скорости автомобиля. Из определения ускорения, следует, что вектор ускорения направлен в ту же сторону, что и разность векторов v – v0. Следовательно в данном случае направление вектора ускорения совпадает с направлением движения тела (с направлением вектора скорости).
Пусть теперь модуль скорости автомобиля уменьшается. В этом случае направление вектора ускорения противоположно направлению движения тела (направлению вектора скорости).
4. Преобразовав формулу ускорения при равноускоренном прямолинейном движении, можно получить формулу для нахождения скорости тела в любой момент времени:
v = at.
5. При вычислении скорости или ускорения пользуются формулами, в которые входят не векторы, а проекции этих величин на координатную ось. Поскольку проекция суммы векторов равна сумме их проекций, то формула для проекции скорости на ось X имеет вид:
vx = v0x + axt,
где vx — проекция скорости в момент времени t, v0x — проекция начальной скорости, ax — проекция ускорения.
При решении задач необходимо учитывать знаки проекций. Так, в случае, изображенном на рисунке проекции скоростей и ускорения на ось X положительны; модуль скорости с течением времени возрастает. В другом случае проекции на ось X скоростей положительны, а проекция ускорения — отрицательна; модуль скорости с течением времени уменьшается.
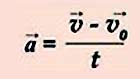
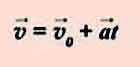
Материал предназначен для учащихся 9-10 классов. Учите, разбирайтесь, готовьтесь решать задачи.
ОтветитьУдалить